As developers, our work is to solve problems which often implies writing code. Some of the problems we face look really simple in nature, but their simplicity leads us to write sub-optimal solutions without even realizing it. JavaScript developers come from very different backgrounds, and assuming that everyone has the same base knowledge of computer science is, at least, misguided. However, we should strive to gain understanding of this field as computer science concepts can help in writing better and more elegant software.
In this article, the first of a series titled From JavaScript developer to JavaScript engineer, I’ll discuss how to re-implement ECMAScript 2015’s String.prototype.repeat() method. What this method does, repeating a string, is pretty simple and a basic implementation would be simple as well. But by using appropriate algorithms and data structures, we can heavily improve the performance of this method.
If you want to take a look at the final solution, you can either go to the section An efficient solution or browse my Interview questions repository on GitHub.
Introducing the String.prototype.repeat() method
ECMAScript 2015 introduces a new method for strings called repeat. The method accepts an integer, that we can refer to as repetitions, and returns a new string that contains the string on which it was called on repeated repetitions amount of times. The value of repetitions is an integer between 0 and +∞, where 0 is included and +∞ is excluded. The method throws a RangeError if the number passed is negative or +∞.
If the behavior of such method is still unclear, here are a few examples of its use:
'*'.repeat(3)returns'***''*'.repeat(0)returns'''*'.repeat(-2)throws aRangeError
To simplify the discussion and the testing, instead of monkey patching the String prototype, I’ll create a function called repeatify() that has the same behavior. The only difference between String.prototype.repeat() and repeatify() is that the latter will accept the string to repeat as its first argument. Therefore, the previous examples will look as shown below:
repeatify('*', 3)returns'***'repeatify('*', 0)returns''repeatify('*', -2)throws aRangeError
Now that I’ve introduced you to the String.prototype.repeat() method, it’s time to implement it.
A simple solution
The problem at hand is so straightforward that even non-experienced developers will be able to solve it in a few minutes. The simplest solution is to start with an empty string that we’ll call result. Then, we copy the string passed as a parameter into it the given amount of times. This step can be achieved by using a for loop. At this point, the only thing left is to address the cases where the repeatify() function has to throw a RangeError exception.
Turning this description into code, results in the following snippet:
function repeatify(string, repetitions) {
if (repetitions < 0 || repetitions === Infinity) {
throw new RangeError('Invalid repetitions number');
}
let result = '';
for (let i = 0; i < repetitions; i++) {
result += string;
}
return result;
}
The code above is easy to write and to read. But is it efficient? It turns out that it only performs well on very small inputs, that is when the value of repetitions is low. As soon as the value of repetitions grows, the execution time of the function increases a lot. If you’re interested in some metrics, take a look at section Performance comparison.
How can we improve the performance of this function? In the next section I’ll answer to this question.
Analysis of the problem
To understand how we can optimize the function, we have to reason about the weak points of the simple solution and build on it.
Strings are immutable
The first point to consider is that strings are immutable. Because of that, every time we concatenate a string to it, a new string is created as a result of our operation. Most applications don’t perform a lot of operations on strings in one go, so the speed of this process can usually be neglected.
Avoid concatenating one string at a time
Another point to take into account is that at every iteration of the loop we perform the same operation: we append the string once. This is not efficient at all.
Let’s suppose that the value of repetitions can only be even. If we assume that, we could create a support string that is made by the string given in input repeated two times. Then, we could speed up the function by running the loop only half of the times by appending the support string. With this idea in mind, it’s easy to account for odd values of repetitions. All we have to do is to add append the original string before returning the result.
Updating the simple solution we’ve discussed in the previous section to embed this change result in the following code:
function repeatify(string, repetitions) {
if (repetitions < 0 || repetitions === Infinity) {
throw new RangeError('Invalid repetitions number');
}
const isEven = repetitions % 2 === 0;
const iterations = Math.floor(repetitions / 2);
const stringTwice = string + string;
let result = '';
for (let i = 0; i < iterations; i++) {
result += stringTwice;
}
if (!isEven) {
result += string;
}
return result;
}
This version is clearly an improvement compared to the first version. We’ve reduced the number of statements executed by the function, thus its execution time. But from the mathematical point of view, the execution time of repeatify() would be still expressed as a linear function. In fact, the function passed from an execution time of O(n) to O(n/2), which can be proved to be a O(n). How can we do better than this?
If you have never heard of the Big O notation, I suggest you to learn more about it. It’s a fundamental concept to analyze the performance of your algorithms.
Splitting the result into chunks
The intuition to concatenate strings made of a given amount of repetitions of the original string that we had in the second version of the function is the key to write a very efficient solution. To understand how our intuition can help, let’s consider the string ****************, obtained by executing repeatify('*', 16). How would you group these characters? One possible way is to split them in half (parenthesis are used to highlight the groups):
(********) (********)
You can surely appreciate that, once we split the string in half, the two resulting chunks are equal. This means that if we build the first chunk, we can then just concatenate it to itself to obtain the final result. But we can go even further. The first string is obtained by splitting it in half and concatenating the result to itself as shown below:
(****) (****) (********)
We can go on and on with this approach until we reach the following result:
(*) (*) (**) (****) (********)
So, if the value of repetitions is a power of 2, we can obtain the final result by creating a string whose initial value is the string passed as an argument, and then concatenating the created string with itself. This approach reduces the amount of operations needed dramatically. In fact, we have to perform only 5 assignments to obtain the same string repeated 16 times. With the simple solution to repeat a string 16 times we have to perform 16 assignments.
Our new approach not only reduces the amount of assignments, but it changes the time complexity of the algorithm. We have passed from an execution time that can be expressed by a linear function to an execution time that can be expressed by a logarithmic function. I’ll cover this topic in more details in the section titled Dealing with repetitions that aren’t power of 2.
To appreciate our gaining, let’s consider a value of repetitions equal to 2048. We have moved from 2048 assignments of the simple solution to just 11 assignments. The image below should also help in visualizing the difference in the operations executed by the three versions discussed in this post.
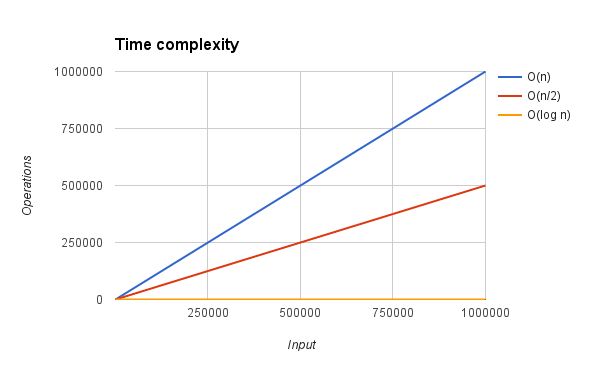
While the new approach works incredibly well for values of repetitions that are power of 2, we haven’t discussed how to deal with all the other values. That’s exactly the purpose of the next section.
Dealing with repetitions that aren’t power of 2
For values of repetitions that are power of 2 we have a very efficient approach. But can we use it to calculate the value for all the other values that repetitions can assume? Yes, we can. Let’s see how by analyzing what happens if we have to produce the string ************************* obtained by running repeatify('*', 25).
We could split the string into half, and then another half, but this isn’t going to lead us anywhere helpful. We would end up dealing with chunks of different sizes and a lot of branches in our code. Instead, let’s start from what we know: we can calculate the first 16 repetitions efficiently. If we do that, we can then focus on calculating the remaining 9 repetitions. But 9 is a number close to a number which is a power of 2, that is 8. And we know that we can calculate these 8 repetitions efficiently as well. So, we’re left with just 1 repetition left (25 – 16 – 8). One repetition is easy to process, but have you pondered that 1 is a power of 2 as well? 1 is in fact equal to 20. This description should suggest that the problem we’re discussing can be solved recursively. At any step we process a given amount of repetitions, then use the same logic to calculate the string for the amount of repetitions left.
In conclusion, we don’t need to have a value of repetitions equal to a power of 2 in input. We can create the final result by building and then concatenating strings that have a size equal to a power of 2. So, the string ************************* can be visualized as follows:
( (*) (*) (**) (****) (********) ) ( (*) (*) (**) (****) ) ( (*) )
This further improvement, results in the function returning the correct result for any input in a time capped by the following formula:
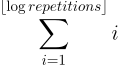
The reason is that the worst case scenario for this approach is that the value of repetitions is a power of 2 minus 1. For instance, numbers like 15 or 2047 are the worst. For such numbers, we have to generate a series of chunks whose lengths create a series of descending powers of 2. If we consider a value of 15 for repetitions, we’ll generate the following chunks:
(********) (****) (**) (*)
As you can see, the lengths of these chunks are 8, 4, 2, and 1.
Now that you know the reason behind the previous formula, you might wonder what its value will be. The exact number of assignments performed by repeatify() can be calculated using the formula to calculate the sum of the first N natural numbers. So, the previous formula can be turned into the following:
![]()
If we had to compute 2047 repetitions and we used the simple version of repeatify(), the function would perform 2047 assignments. On the contrary, this latest version would only perform 66 assignments. This is great, but it turns out that we can do even better than this.
By looking at the simple diagram above, you might notice that the first chunk (the one made of 16 repetitions of the original string) is the biggest. All the subsequent chunks will always be smaller in size. As I mentioned before, we generate a series of chunks whose lengths create a series of descending powers of 2. This means that the biggest processing effort is made to calculate the first chunk. Moreover, you might notice that we’re creating the same chunks multiple times as big chunks are made of smaller chunks concatenated with themselves. A cache can help us in further improving our solution.
Using memoization to avoid reprocessing the same chunks
Memoization is a technique to store the return value of a function, given some inputs, so that it doesn’t need to be recalculated.
We can employ this technique to store the chunk created at every iteration so that we don’t have to recalculate it if needed. And we now know that we’ll need to recreate the same chunks multiple times. By employing memoization we can avoid this waste of computational power. As a result, the execution time of the repeatify() will become an O(log repetitions), and even more a Θ(log repetitions).
To give you an idea of how much we have improved the performance of the algorithm, consider that for a value of repetitions equal to 2047, the simple solution performs 2047 assignments. On the contrary, an implementation that takes into account all the considerations described only needs 11 assignments.
With this last improvement, we are finally ready to implement a better solution. If you want to see some metrics about how much the first solution and the efficient solution compares, have a look at the section titled Performance comparison.
An efficient solution
Thanks to our analysis of the problem, we’re now ready to implement an efficient version of the repeatify() function.
To start, we handle the cases where the function has to throw an exception.
if (repetitions < 0 || repetitions === Infinity) {
throw new RangeError('Invalid repetitions number');
}
Once done, we need to create the cache where we’ll store the values calculated. We also need to setup the recursive function that we’ll use to solve problems with inputs smaller in size at every call.
const cache = new Map();
function repeat(string, repetitions) {
// To implement
}
return repeat(string, repetitions);
Let’s now focus on the core of the algorithm. The first step is to calculate how long the chunk we’re processing at any call of the repeat() will be. As discussed before, this number is equal to the floor of the logarithm base 2 of repetitions. At this point, two things can happen. One possibility is that the chunk we’ve to build has already been created and it’s stored in our cache. The other possibility is that we’ve to build it. If the chunk isn’t in the cache, we’ll take the chance to store every partial result (chunk) in the cache so that we’ll avoid any future reprocessing of the same string. The base case occurs when the number of repetitions is equal to zero. In this case we have to return an empty string.
if (repetitions === 0) {
return '';
}
const log = Math.floor(Math.log2(repetitions));
let result;
if (cache.has(log)) {
result = cache.get(log);
} else {
result = string;
for (let i = 1; i <= log; i++) {
result += result;
cache.set(i, result);
}
}
The last step is to calculate if there are other chunks of the final result to calculate. If so, we concatenate the current partial result with whatever will be the result of the recursive call to repeat(). Such recursive call will have a value of repetitions equal to the number of repetitions we’ve yet to calculate.
const repetitionsProcessed = Math.pow(2, log); const repetitionsLeft = repetitions - repetitionsProcessed; return result + repeat(string, repetitionsLeft);
The final version of the repeatify() function can be found in my repository Interview questions repository on GitHub and it’s also listed below:
function repeatify(string, repetitions) {
if (repetitions < 0 || repetitions === Infinity) {
throw new RangeError('Invalid repetitions number');
}
const cache = new Map();
function repeat(string, repetitions) {
if (repetitions === 0) {
return '';
}
const log = Math.floor(Math.log2(repetitions));
let result;
if (cache.has(log)) {
result = cache.get(log);
} else {
result = string;
for (let i = 1; i <= log; i++) {
result += result;
cache.set(i, result);
}
}
const repetitionsProcessed = Math.pow(2, log);
const repetitionsLeft = repetitions - repetitionsProcessed;
return result + repeat(string, repetitionsLeft);
}
return repeat(string, repetitions);
}
As you can see, the final version of the function is more complex than the first one. The simplicity of the first solution lets it perform well for small input. The reason is that the final version calculates different elements before running the core of the algorithm. However, the structure of the final version pays back when the value of repetitions exceeds a certain threshold.
bind() which used to be slow and now is much faster.
In the next section, I’ll unveil some data so that you can visualize the difference.
Performance comparison
While analyzing the repeatify() function, we have implemented different versions of it. Along the way, we’ve also discussed how faster the final version improves the performance compared to the first one. In this section, I want to present you some data so that you can visualize the improvement.
The table below shows the number of statements of the two versions for different values of repetitions. The data reported here ignores the statements that are always executed, such as the if at the beginning of the function and the return statement, to focus on the core part of the two functions:
| Repetitions | Simple | Final |
|---|---|---|
| 1 | 1 | 1 |
| 10 | 10 | 4 |
| 100 | 100 | 8 |
| 1000 | 1000 | 14 |
| 10000 | 10000 | 17 |
| 100000 | 100000 | 21 |
| 1000000 | 1000000 | 37 |
The second table reports the execution times of both the solutions. To calculate them, I used the High Resolution Time API to retrieve the current time in milliseconds, with the microseconds in the fractional part. Moreover, in order to have a more accurate estimation, I’ve executed both the functions for 100000 times and calculated the average execution time for each value of repetitions.
| Repetitions | Simple | Final |
|---|---|---|
| 1 | 0.0005739500000000566 | 0.0012151499999999617 |
| 10 | 0.001580399999999994 | 0.0016651500000001112 |
| 100 | 0.004197299999999895 | 0.001874350000000004 |
| 1000 | 0.023017249999999916 | 0.0029845999999998573 |
| 10000 | 0.2496317500000012 | 0.003155000000000075 |
| 100000 | 2.745029200000003 | 0.004887150000000115 |
| 1000000 | 126.05984999999997 | 0.005735250000000005 |
By looking at these tables you can see the benefits obtained with our refinement. As the value of repetitions grows, the amount of operations performed by the final version of the function is far smaller than those performed by the simple version. The huge difference in performance can also be noticed by looking at the execution times. For a value of repetitions of 1000000, the final version is ~25000 times faster than the simple version.
For small values of repetitions the two versions have almost the same performance, while for very small values the simple version is even faster. The reason for these times is that the final version has a more complex setup, and the cache system we put in place only becomes effective with large values.
Is the final version worth it?
The data I provided in the previous section clearly shows how efficient the final solution is. But the improvement in performance only becomes meaningful for very high values of repetitions. In addition, the final version is definitely harder to read and understand than the simple solution. So, you might wonder if all that complexity is worth the effort. It depends™ on your context.
If your application rarely invokes the function and it does by passing very small values of repetitions, then the simple solution might be the way to go. In such cases, the difference in performance is negligible and you’ll benefit from a simpler and more concise code. On the contrary, if the function is called very often, perhaps with values of repetitions that are high, if you’re working on a real-time application where every millisecond matters, or if your most important devices don’t have a lot of computational power, then you should definitely employ the final solution.
Conclusions
In this first article of my series From JavaScript developer to JavaScript engineer, I’ve used ECMAScript 2015’s String.prototype.repeat() method to highlight the importance of using appropriate algorithms and data structures when writing code. As discussed, during our work we might face problems that are simple but lead us to write sub-optimal solutions.
While this post discusses a specific example, I covered several important topics that you can and should consider when creating software. In particular, I’ve explained recursion, memoization, big O and big Theta notations to calculate the time complexity of the two solutions provided. These are notions that every (JavaScript) developer should master.
Having knowledge of the mathematical notations used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity helps in understanding if a solution is more efficient than other(s). Calculating the time complexity of an algorithm often helps in finding its weak points so that you can improve it.